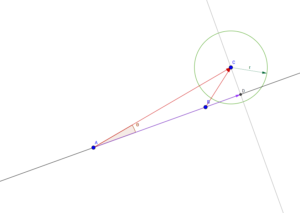
[:en]Collision between Segment AB and circle C (radius r). Let’s remember a little of vector algebra and pythagorean theorem.
The height of the right-angle triangle ACD is what we need to compare with radius.

[latex]
\vec{AD} \text{ is the projection of } \vec{AC} \text{, the base of triangle }ACD \\
\vec{AD} = \vec{AC} \ cos \theta \\
\text{Vector dot product:} \\
\vec{AC}\cdot\vec{AB} = cos \theta *\left | \vec{AC} \right | * \left |\vec{AB} \right | \text{ geometrically } \\
\vec{AC}\cdot\vec{AB} = ac_x*ab_x + ac_y*ab_y \text{ algebraically} \\
cos \theta *\left | \vec{AC} \right | * \left |\vec{AB} \right | = ac_x*ab_x + ac_y*ab_y \\
\text { use normalized (length = 1) vector } \hat{AB} \ ( \hat{AB} = \vec{AB} \div \left | \vec{AB} \right | ) \\
cos \theta *\left | \vec{AC} \right | = ac_x*\hat{ab}_x + ac_y*\hat{ab}_y \\
cos \theta *\left | \vec{AC} \right | = \left | \vec{AD} \right | \text{, triangle base length} \\
\text{Pythagoras} \left | \vec{AC} \right |^2 = \left | \vec{AD} \right |^2 + height^2 \\
radius \geq height \ \Rightarrow \text{collision} \\
height ^2 = \left | \vec{AC} \right |^2 – \left | \vec{AD} \right |^2\\
\text{compare } height^2 \text{ to avoid } \sqrt{height} \\
\text{This can be used when the height of the triangle fall inside the segment } \overline{AB} \\
0 \leq \left | \vec{AD} \right | \leq \left | \vec{AB} \right |
[/latex]
This is a segment and not an infinite line; When the triangle height fall outside of the segment (look at the picture aside, height < radius but still no collision) we can compare directly length of the two vectors AC and AB with radius; It’s better comparing squared length.
bool Polyline::segmentCollideWithCircle(QPointF C, qreal radius, QPointF A, QPointF B)
{
QVector2D AB(A-B);
QVector2D CB(C-B);
qreal proj = QVector2D::dotProduct(AB.normalized(),CB); // |AB|*cos Theta (projection length)
if (proj>0 && proj<AB.length()) return (radius*radius > CB.length() * CB.length() - proj*proj);
if (radius > CB.length() || radius > QVector2D(A-C).length()) return true;
return false;
}
[:]